A better hash table: Clang

After Microsoft Visual Studio 2012 and GCC 4.8.2, we now provide the results of our performance test suite for C++ unordered associative containers in Clang 3.4. All the tests were compiled and run by Thomas Goyne on a Mac OS X 10.9.1 box with an Intel Core i7-3720QM @2.6GHz, Turbo Boost and SpeedStep disabled, release settings -O3 -std=c++11.

Clang can work with two different standard libraries, libstdc++-v3 and libc++: we have tried both libstdc++ 4.8.2 and libc++ 3.4.

libstdc++-v3

Insertion without rehashing, unique elements.

Insertion with rehashing, unique elements.

Insertion without rehashing, duplicate elements, F_max = 1, G = 5.

Insertion without rehashing, duplicate elements, F_max = 5, G = 5.

Insertion with rehashing, duplicate elements, F_max = 1, G = 5.

Insertion with rehashing, duplicate elements, F_max = 5, G = 5.

Erasure, unique elements.

Erasure, duplicate elements, F_max = 1, G = 5.

Erasure, duplicate elements, F_max = 5, G = 5.

Successful lookup, unique elements.

Unsuccessful lookup, unique elements.

Successful lookup, duplicate elements, F_max = 1, G = 5.

Unsuccessful lookup, duplicate elements, F_max = 1, G = 5.

Successful lookup, duplicate elements, F_max = 5, G = 5.

Unsuccessful lookup, duplicate elements, F_max = 5, G = 5.

As expected, the results are very similar to those obtained with GCC: the only noteworthy difference is Boost.Unordered performance in lookup with unique elements, which is somewhat poorer here —the reasons for this discrepancy are not clear to me.

libc++

Insertion without rehashing, unique elements.

Insertion with rehashing, unique elements.

Insertion without rehashing, duplicate elements, F_max = 1, G = 5.

Insertion without rehashing, duplicate elements, F_max = 5, G = 5.

Insertion with rehashing, duplicate elements, F_max = 1, G = 5.

Insertion with rehashing, duplicate elements, F_max = 5, G = 5.

Erasure, unique elements.

Erasure, duplicate elements, F_max = 1, G = 5.

Erasure, duplicate elements, F_max = 5, G = 5.

Successful lookup, unique elements.

Unsuccessful lookup, unique elements.

Successful lookup, duplicate elements, F_max = 1, G = 5.

Unsuccessful lookup, duplicate elements, F_max = 1, G = 5.

Successful lookup, duplicate elements, F_max = 5, G = 5.

Unsuccessful lookup, duplicate elements, F_max = 5, G = 5.

In general, the unordered associative containers provided by libc++ are considerably slower than those in libstdc++-v3:

• When duplicate elements are allowed, insertion of a new element in libc++ takes place at the end of the range of equivalent elements (in libstdc++ -v3 it is at the beginning), which incurs the extra cost of traversing the range.
• Erasure is unnecessarily expensive: to determine whether a given node p is located at the beginning of its bucket b, libc++ does a hash→bucket mapping on the predecessor prev of x and checks if the resulting bucket is not the same as b, when it suffices to verify if b points to prev.
• It is harder to explain why lookup (specially with unique elements) is so much slower than in libstdc++-v3: code inspection reveals that the hash→bucket mapping is less efficient in libc++ (it involves one extra logical and operation), but this fact alone seems unlikely to account for the big differences in performance.

A better hash table: GCC

As a continuation of our previous entry in the performance of various implementations of C++ unordered associative containers, Thomas Goyne has run the measurement test suite in GCC 4.8.2 for Mac with the default standard library libstdc++-v3 and release settings -O3 -std=c++11. The machine used was a OS X 10.9.1 box with an Intel Core i7-3720QM running at 2.6GHz with Turbo Boost and SpeedStep disabled. Results are depicted below.

Insertion without rehashing, unique elements.

Insertion with rehashing, unique elements.

Insertion without rehashing, duplicate elements, F_max = 1, G = 5.

Insertion without rehashing, duplicate elements, F_max = 5, G = 5.

Insertion with rehashing, duplicate elements, F_max = 1, G = 5.

Insertion with rehashing, duplicate elements, F_max = 5, G = 5.

Erasure, unique elements.

Erasure, duplicate elements, F_max = 1, G = 5.

Erasure, duplicate elements, F_max = 5, G = 5.

Successful lookup, unique elements.

Unsuccessful lookup, unique elements.

Successful lookup, duplicate elements, F_max = 1, G = 5.

Unsuccessful lookup, duplicate elements, F_max = 1, G = 5.

Successful lookup, duplicate elements, F_max = 5, G = 5.

Unsuccessful lookup, duplicate elements, F_max = 5, G = 5.

Some general insights:

• Insertion times are very similar among the three libs for unique elements. As for the case of duplicate elements, the group skipping capabilities of Boost.Unordered and Boost.MultiIndex, while greatly improving lookup performance, do have a noticeable negative impact on insertion times.
• On the other hand, libstdc++-v3 performs surprisingly well in erasure with duplicate elements, despite its having to do bucket traversal to locate the node preceding the one to be erased. I don't have a clear explanation for this fact besides attributing it to a better CPU cache behavior due to element nodes in libstdc++-v3 being smaller (as this lib does not store hash values if these can be calculated on the fly): maybe readers can propose alternative interpretations.
• Boost.Multiindex highest locality shows up very clearly in its excellent lookup performance for unique elements.

At a later entry we will study libstdc++-v3, libc++, Boost.Unordered and Boost.MultiIndex in Clang.

A better hash table

In previous entries we have described several implementations of C++ unordered associative containers without and with duplicate elements. Subsequent performance measurements have taught us how important algorithm locality is in the presence of CPU memory caches, which favor data structures with as few node indirections as possible. This suggests an improvement over the implementation introduced by Boost.MultiIndex hashed indices for Boost 1.56. In the case of unique elements, the data structure looked like this:

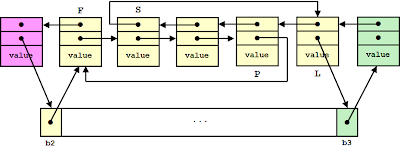
Let us now twist this structure a bit:

This new scheme results from the old one by merely swapping forward and back pointers (bucket nodes are equipped then with back pointers), which at first blush seems to gain us nothing in terms of efficiency. But there is a key difference: going from a bucket node to the first bucket element is now done directly, rather than with an indirection through the preceding node. Previously, traversing a bucket of n elements required visiting 1 bucket node and n + 2 element nodes; with the new implementation, 2 bucket nodes and n element nodes, one less node in total (and visiting bucket nodes is expected to be cheaper, as they lie contiguously in an array and are thus better cached). Similarly, insertion of an element at the beginning of a nonempty bucket involves visiting 2 nodes while formerly it involved 3, and if the bucket is empty (this is harder to see) it is 4 vs. 5 nodes.

The same change can be easily applied to the case of duplicate elements, from:

to

This seemingly small modification brings about substantial improvements in performance. We have repeated the measurements done in the series of articles

• Measuring insertion times for C++ unordered associative containers
• Measuring insertion times for C++ unordered associative containers with duplicate elements
• Measuring erasure times for C++ unordered associative containers
• Measuring lookup times for C++ unordered associative containers

under the same conditions as described there. For the reader's reference, we provide snaphots to

• Boost.MultiIndex for Boost 1.56, prerelease 1 (the one used for the first set of measurements),
• Boost.MultiIndex for Boost 1.56, prerelease 2, (with the changes proposed in this entry).

Besides the change in data structure, prerelease 2 of Boost.MultiIndex also includes some improvements in its rehashing procedure. The new results are depicted below.

Insertion without rehashing, unique elements.

Insertion with rehashing, unique elements.

Insertion without rehashing, duplicate elements, F_max = 1, G = 5.

Insertion without rehashing, duplicate elements, F_max = 5, G = 5.

Insertion with rehashing, duplicate elements, F_max = 1, G = 5.

Insertion with rehashing, duplicate elements, F_max = 5, G = 5.

Erasure, unique elements.

Erasure, duplicate elements, F_max = 1, G = 5.

Erasure, duplicate elements, F_max = 5, G = 5.

Successful lookup, unique elements.

Unsuccessful lookup, unique elements.

Successful lookup, duplicate elements, F_max = 1, G = 5.

Unsuccessful lookup, duplicate elements, F_max = 1, G = 5.

Successful lookup, duplicate elements, F_max = 5, G = 5.

Unsuccessful lookup, duplicate elements, F_max = 5, G = 5.

Note that implementations of C++ unordered associative containers based on single linking cannot apply this improvement, that is, they cannot make bucket nodes point directly to the first element in the bucket: if they did so, the node preceding the first in a bucket would be unreachable in constant time, making it impossible to efficiently implement erasure.