Comparing the run-time performance of Fil-C and ASAN

After the publication of the experiments with Boost.Unordered on Fil-C, some readers asked for a comparison of run-time performances between Fil-C and Clang's AddressSanitizer (ASAN).

Warning

Please do not construe this article as implying that Fil-C and ASAN are competing technologies within the same application space. Whereas ASAN is designed to detect bugs resulting in memory access violations, Fil-C sports a stricter notion of memory safety including UB situations where a pointer is directed to a valid memory region that is nonetheless out of bounds with respect to the pointer's provenance. That said, there's some overlapping between both tools, so it's only natural to question about their relative impact on execution times.

Results

Our previous benchmarking repo has been updated to include results for plain Clang 18, Clang 18 with ASAN enabled, and Fil-C v0.674, all with release mode settings. The following figures show execution times in ns per element for Clang/ASAN (solid lines) and Fil-C (dashed lines) for three Boost.Unordered containers (boost::unordered_map,  boost::unordered_flat_map and boost::unordered_node_map) and four scenarios.

Running insertion	Running erasure

Successful lookup	Unsuccessful lookup

In summary:

• Insertion:
  Fil-C is between 1.8x slower and 4.1x faster than ASAN (avg. 1.3x faster).
• Erasure:
  Fil-C is between 1.3x slower and 9.2x faster than ASAN (avg. 1.9x faster).
• Successful lookup:
  Fil-C is between 2.5x slower and 1.9x faster than ASAN (avg. 1.6x slower).
• Unsuccessful lookup:
  Fil-C is between 2.6x slower  and 1.4x faster than ASAN (avg. 1.9x slower).

So, results don't allow us to establish a clear-cut "winner". When allocation/deallocation is involved, Fil-C seems to perform better (except for insertion when the memory working set gets past a certain threshold). For lookup, Fil-C is generally worse, and, again, the gap increases as more memory is used. A deeper analysis would require knowledge of the internals of both tools that I, unfortunately, lack.

Some experiments with Boost.Unordered on Fil-C

Fil-C is a C and C++ compiler built on top of LLVM that adds run-time memory-safety mechanisms preventing out-of-bounds and use-after-free accesses. This naturally comes at a price in execution time, so I was curious about how much of a penalty that is for a performance-oriented, relatively low-level library like Boost.Unordered.

Compiling and testing

From the user's perspective, Fil-C is basically a Clang clone, so it is fairly easy to integrate in previously existing toolchains. This repo shows how to plug Fil-C into Boost.Unordered's CI, which runs on GitHub Actions and is powered by Boost's own B2 build system. The most straightforward way to make B2 use Fil-C is by having a user-config.jam file like this:

using clang : : fil++ ;

which instructs B2 to use the clang toolset with the only change that the compiler name is not the default clang++ but fil++.

We've encountered only minor difficulties during the process:

•  In the enviroment used (Linux x64), B2 automatically includes --target=x86_64-pc-linux as part of the commandline, which confuses the adapted version of libc++ shipping with Fil-C. This option had to be overridden with --target=x86_64-unknown-linux-gnu (which is the default for Clang).
• As of this writing, Fil-C does not accept inline assembly code (asm or __asm__ blocks), which Boost.Unordered uses to provide embedded GDB pretty-printers. The feature was disabled with the macro BOOST_ALL_NO_EMBEDDED_GDB_SCRIPTS. 

Other than this, the extensive Boost.Unordered test suite compiled and ran successfully, except for some tests involving Boost.Interprocess, which uses inline assembly in some places. CI completed in around 2.5x the time it takes with a regular compiler. It is worth noting that Fil-C happily accepted SSE2 SIMD intrinsics crucially used by Boost.Unordered.

Run-time performance

We ran some performance tests compiled with Fil-C v0.674 on a Linux machine, release settings (benchmark code and setup here). The figures show execution times in ns per element for Clang 15 (solid lines) and Fil-C (dashed lines) and three containers: boost::unordered_map (closed-addressing hashmap), and boost::unordered_flat_map and boost::unordered_node_map (open addressing).

Running insertion	Running erasure

Successful lookup	Unsuccessful lookup

Execution with Fil-C is around 2x-4x slower, with wide variations depending on the benchmarked scenario and container of choice. Closed-addressing boost::unordered_map is the container experiencing the largest degradation, presumably because it does the most amount of pointer chasing.

Bulk operations in Boost.Bloom

Starting in Boost 1.90, Boost.Bloom will provide so-called bulk operations, which, in general, can speed up insertion and lookup by a sizable factor. The key idea behind this optimization is to separate in time the calculation of a position in the Bloom filter's array from its actual access. For instance, if this is the the algorithm for regular insertion into a Bloom filter with k = 1 (all the snippets in this article are simplified, illustrative versions of the actual source code):

void insert(const value_type& x)
{
  auto h = hash(x);
  auto p = position(h);
  set(position, 1);
}

then the bulk-mode variant for insertion of a range of values would look like:

void insert(const std::array<value_type, N>& x)
{
  std::size_t positions[N];
  
  // pipeline position calculation and memory access
  
  for(std::size_t i = 0; i < N; ++i) {
    auto h = hash(x[i]);
    positions[i] = position(h);
    prefetch(positions[i]);
  }
  
  for(std::size_t i = 0; i < N; ++i) {
    set(positions[i], 1);
  }
}

By prefetching the address of positions[i] way in advance of its actual usage in set(positions[i], 1), we make sure that the latter is accessing a cached value and avoid (or minimize) the CPU stalling that would result from reaching out to cold memory. We have studied bulk optimization in more detail in the context of boost::concurrent_flat_map. You can see actual measurements of the performance gains achieved in a dedicated repo; as expected, gains are higher for larger bit arrays not fitting in the lower levels of the CPU's cache hierarchy.

From an algorithmic point of view, the most interesting case is that of lookup operations for k > 1, since the baseline non-bulk procedure is not easily amenable to pipelining:

bool may_contain(const value_type& x)
{ 
  auto h = hash(x);
  for(int i = 0; i < k; ++i) {
    auto p = position(h);
    if(check(position) == false) return false;
    if(i < k - 1) h = next_hash(h);
  }
  return true;
}

This algorithm is branchful and can take anywhere from 1 to k iterations, the latter being the case for elements present in the filter and false positives. For instance, this diagram shows the number of steps taken to look up n = 64 elements on a filter with k = 10 and FPR = 1%, where the successful lookup rate (proportion of looked up elements actually in the filter) is p = 0.1:

As it can be seen, for non-successful lookups may_contain typically stops at the first few positions: the average number of positions checked (grayed cells) is  \[n\left(pk +(1-p)\frac{1-p_b^{k}}{1-p_b}\right),\] where \(p_b=\sqrt[k]{\text{FPR}}\) is the probability that an arbitrary bit in the filter's array is set to 1. In the example used, this results in only 34% of the total nk = 640 positions being checked.

Now, a naïve bulk-mode version could look as follows:

template<typename F>
void may_contain(
  const std::array<value_type, N>& x,
  F f) // f is fed lookup results
{ 
  std::uint64_t hashes[N];
  std::size_t   positions[N];
  bool          results[N];
  
  // initial round of hash calculation and prefetching
  
  for(std::size_t i = 0; i < N; ++i) {
    hashes[i] = hash(x[i]);
    positions[i] = position(hashes[i]);
    results[i] = true;
    prefetch(positions[i]);
  }
  
  // main loop
  
  for(int j = 0; j < k; ++i) {
    for(std::size_t i = 0; i < N; ++i) {
      if(results[i]) { // conditional branch X
        results[i] &= check(positions[i]);
        if(results[i] && j < k - 1) {
          hashes[i] = next_hash(hashes[i]);
          positions[i] = position(hashes[i]);
          prefetch(positions[i]);
        }
      }
    }
  }
  
  // feed results
  
  for(int i = 0; i < k; ++i) {
    f(results[i]);
  }
}

This simply stores partial results in an array and iterates row-first instead of column-first:

The problem with this approach is that, even though it calls check exactly the same number of times as the non-bulk algorithm, the conditional branch labeled X is executed \(nk\) times, and this has a huge impact on the CPU's branch predictor. Conditional branches could in principle be eliminated altogether:

for(int j = 0; j < k; ++i) {
  for(std::size_t i = 0; i < N; ++i) {
    results[i] &= check(positions[i]);
    if(j < k - 1) { // this check is optimized away at compile time
      hashes[i] = next_hash(hashes[i]);
      positions[i] = position(hashes[i]);
      prefetch(positions[i]);
    }
  }
}

but this would result in \(nk\) calls to check for ~3 times more computational work than the non-bulk version.

The challenge then is to reduce the number of iterations on each row to only those positions that still need to be evaluated. This is the solution adopted by Boost.Bloom:

template<typename F>
void may_contain(
  const std::array<value_type, N>& x,
  F f) // f is fed lookup results
{ 
  std::uint64_t hashes[N];
  std::size_t   positions[N];
  std::uint64_t results = 0; // mask of N bits
  
  // initial round of hash calculation and prefetching
  
  for(std::size_t i = 0; i < N; ++i) {
    hashes[i] = hash(x[i]);
    positions[i] = position(hashes[i]);
    results |= 1ull << i;
    prefetch(positions[i]);
  }
  
  // main loop
  
  for(int j = 0; j < k; ++i) {
    auto mask = results;
    if(!mask) break;
    do{
      auto i = std::countr_zero(mask);
      auto b = check(positions[i]);
      results &= ~(std::uint64_t(!b) << i);
      if(j < k - 1) { // this check is optimized away at compile time
        hashes[i] = next_hash(hashes[i]);
        positions[i] = position(hashes[i]);
        prefetch(positions[i]);
      }
      mask &= mask - 1; // reset least significant 1
    } while(mask);
  }
  
  // feed results
  
  for(int i = 0; i < k; ++i) {
    f(results & 1);
    results >>= 1;
  }
}

Instead of an array of partial results, we keep these as a bitmask, so that we can skip groups of terminated columns in constant time using std::countr_zero. For instance, in the 7th row the main loop does 11 iterations instead of n = 64.

In summary, the bulk version of may_contain only does n more conditional branches than the non-bulk version, plus \(n(1-p)\) superfluous memory fetches —the latter could be omitted at the expense of \(n(1-p)\) additional conditional branches, but benchmarks showed that the version with extra memory fetches is actually faster. These are measured speedups of bulk vs. non-bulk lookup for a boost::bloom::filter<int, K> containing 10M elements under GCC, 64-bit mode:

array size	K	p = 1	p = 0	p = 0.1
8M	6	0.78	2.11	1.43
12M	9	1.54	2.27	1.38
16M	11	2.08	2.45	1.46
20M	14	2.24	2.57	1.43

(More results here.)

Conclusions

Boost.Bloom will introduce bulk insertion and lookup capabilities in Boost 1.90, resulting in speedups of up to 3x, though results vary greatly depending on the filter configuration and its size, and may even have less performance than the regular case in some situations. We have shown how bulk lookup is implemented for the case k > 1, where the regular, non-bulk version is highly branched and so not readily amenable to pipelining. The key technique, based on iteration reduction with std::countr_zero, can be applied outside the context of Boost.Bloom to implement efficient pipelining of early-exit operations.

Maps on chains

(From a conversation with Vassil Vassilev.) Suppose we want to have a C++ map where the keys are disjoint, integer intervals of the form [a, b]:

struct interval
{
  int min, max;
};

std::map<interval, std::string> m;

m[{0, 9}] = "ABC";
m[{10, 19}] = "DEF";

This looks easy enough, we just have to write the proper comparison operator for intervals, right?

bool operator<(const interval& x, const interval& y)
{
  return x.max < y.min;
}

But what happens if we try to insert an interval which is not disjoint with those already in the map?

m[{5, 14}] = "GHI"; // intersects both {0, 9} and {10, 19}

The short answer is that this is undefined behavior, but let's try to undertand why. C++ associative containers depend on the comparison function (typically, std::less<Key>) inducing a so-called strict weak ordering on elements of Key. In layman terms, a strict weak order < behaves as the "less than" relationship does for numbers, except that there may be incomparable elements x, y such that x ≮ y and y ≮ x; for numbers, this only happens if x = y, but in the case of a general SWO we allow for distinct, incomparable elements as long as they form equivalence classes. A convenient way to rephrase this condition is to require that incomparable elements are totally equivalent in how they compare to the rest of the elements, that is, they're truly indistinguishable from the point of view of the SWO. Getting back to our interval scenario, we have three possible cases when comparing [a, b] and [c, d]:

• If b < c, the intervals don't overlap and [a, b] < [c, d].
• If d < a, the intervals don't overlap and [c, d] < [a, b].
• Otherwise, the intervals are incomparable. This can happen when [a, b] and [c, d] overlap partially or when they are exactly the same interval.

What we have described is a well known relationship called interval order. The problem is that the interval order is not a strict weak order. Let's depict a Hasse diagram for the interval order on integer intervals [a,b] between 0 and 4:

A Hasse diagram works like this: given two elements x and y, x < y iff there is a path going upwards that connects x to y. For instance, the fact that [1, 1] < [3, 4] is confirmed by the path [1, 1] → [2, 2] → [3, 4]. But the diagram also serves to show why this relationship is not a strict weak order: for it to be so, incomparable elements (those not connected) should be indistinguishable in that they are connected upwards and downwards with the same elements, and this is clearly not the case (in fact, it is not the case for any pair of incomparable elements). In mathematical terms, our relationship is of a more general type called a strict partial order.

Going back to C++, associative containers assume that the elements inserted form a linear arrangement with respect to <: when we try to insert a new element y that is incomparable with some previously inserted element x, the properties of strict weak orders allows us to determine that x and y are equivalent, so nothing breaks up (the insertion fails as a duplicate for a std::map, or y is added next to x for a std::multimap).

There's a way to accommodate our interval scenario with std::map, though. As long as the elements we are inserting belong to the same connecting path or chain, std::map can't possibly "know" if our relationship is a strict weak order or not: it certainly looks like one for the limited subset of elements it has seen so far. Implementation-wise, we just have to make sure we're not comparing partially overlapping intervals:

struct interval_overlap: std::runtime_error
{
  interval_overlap(): std::runtime_error("interval overlap"){}
};

bool operator<(const interval& x, const interval& y)
{
  if(x.min == y.min) {
    if(x.max != y.max) throw interval_overlap();
    return false;
  }
  else if(x.min < y.min) {
    if(x.max >= y.min) throw interval_overlap();
    return true;
  }
  else /* x.min > y.min */
  {
    if(x.min <= y.max) throw interval_overlap();
    return false;
  }
}

std::map<interval, std::string> m;

m[{0, 9}] = "ABC";
m[{10, 19}] = "DEF";
m[{5, 14}] = "GHI"; // throws interval_overlap

So, when we try to insert an element that would violate the strict weak ordering constraints (that is, it lies outside the chain connecting the intervals inserted so far), an exception is thrown and no undefined behavior is hit. A strict reading of the standard would not allow this workaround, as it is required that the comparison object for the map induce a strict weak ordering for all possible values of Key, not only those in the container (or that is my interpretation, at least): for all practical purposes, though, this works and will foreseeably continue to work for all future revisions of the standard.

Bonus point. Thanks to heterogeneous lookup, we can extend our use case to support lookup for integers inside the intervals:

struct less_interval
{
  using is_transparent = void;

  bool operator()(const interval& x, const interval& y) const
  {
    // as operator< before
  }

  bool operator()(int x, const interval& y) const
  {
    return x < y.min;
  }
  
  bool operator()(const interval& x, int y) const
  {
    return x.max < y; 
  }    
};

std::map<interval, std::string, less_interval> m;
  
m[{0, 9}] = "ABC";
m[{10, 19}] = "DEF";

std::cout << m.find(5)->second << "\n"; // prints "ABC"

Exercise for the reader: Can you formally prove that this works? (Hint: define a strict weak order on ℕ ∪ I, where ℕ is the set of natural numbers and I is a collection of disjoint integer intervals.)

WG21, Boost, and the ways of standardization

• Goals of standardization
• Standardizing programming languages
• WG21
• Innovation vs. adoption
• Pros and cons of standardization
• An assessment model for library standardization
• Boost, the standard and beyond
• Golden era: 1998-2011
• Middle-age issues: 2012-2020
• Evolution: 2021-2024 and the future
• Conclusions
  

Goals of standardization

Standardization, in a form resembling our contemporary practices, began in the Industrial Revolution as a means to harmonize incipient mass production and their associated supply chains through the concept of interchangeability of parts. Some early technical standards are the Gribeauval system (1765, artillery pieces) and the British Standard Whitworth (1841, screw threads). Taylorism expanded standardization efforts from machinery to assembly processes themselves with the goal of increasing productivity (and, it could be said, achieving interchangeability of workers). Standards for metric systems, such as that of Revolutionary France (1791) were deemed "scientific" (as befitted the enlightenment spirit of the era) in that they were defined by exact, reproducible methods, but their main motivation was to facilitate local and international trade rather than support the advancement of science. We see a common theme here: standardization normalizes or leverages technology to favor industry and trade, that is, technology precedes standards.

This approach is embraced by 20th century standards organizations (DIN 1917, ANSI 1918, ISO 1947) through the advent of electronics, telecommunications and IT, and up to our days. Technological advancement, or, more generally, innovation (a concept coined around 1940 and ubiquitous today) is not seen as the focus of standardization, even though standards can promote innovation by consolidating advancements and best practices upon which further cycles of innovation can be built —and potentially be standardized in their turn. This interplay between standardization and innovation has been discussed extensively within standards organizations and outside. The old term "interchangeability of parts" has been replaced today by the more abstract concepts of compatibility, interoperability and (within the realm of IT) portability.

Standardizing programming languages

Most programming languages are not officially standardized, but some are. As of today, these are the ISO-standardized languages actively maintained by dedicated working groups within the ISO/IEC JTC1/SC22 subcommittee for programming languages:

• COBOL (WG4)
• Fortran (WG5)
• Ada (WG9)
• C (WG14)
• Prolog (WG17)
• C++ (WG21)
  

What's the purpose of standardizing a programming language? JC22 has a sort of foundational paper which centers on the benefits of portability, understood as both portability across systems/environments and portability of people (a rather blunt allusion to old-school Taylorism). The paper does not mention the subject of implementation certification, which can play a significant role for languages such as Ada that are used in heavily regulated sectors. More importantly to our discussion, it does not either mention what position SC22 holds with respect to innovation: regardless, we will see that innovation does indeed happen within SC22 workgroups, in what represents a radical departure from classical standardization practices.

WG21

C++ was mostly a one man's effort since its inception in the early 80s until the publication of The Annotated C++ Reference Manual (ARM, 1990), which served as the basis for the creation of an ANSI/ISO standardization committee that would eventually release its first C++ standard in 1998. Bjarne Stroustrup cited avoidance of compiler vendor lock-in (a variant of portability) as a major reason for having the language standardized —a concern that made much sense in a scene then dominated by company-owned languages such as Java.

Innovation was seen as WG21's business from its very beginning: some features of the core language, such as templates and exceptions, were labeled as experimental in the ARM, and the first version of the standard library, notably including Alexander Stepanov's STL, was introduced by the committee in the 1990-1998 period with little or no field experience. After a minor update to C++98 in 2003, the innovation pace picked up again in subsequent revisions of the standard (2011, 2014, 2017, 2020, 2023), and the current innovation backlog does not seem to falter; if anything, we could say that the main blocker for innovation within the standard is lack of human resources in WG21 rather than lack of proposals.

Innovation vs. adoption

Not all new features in the C++ standard have originated within WG21. We must distinguish here between the core language and the standard library:

• External innovation in the core language is generally hard as it requires writing or modifying a C++ compiler, a task outside the capabilities of many even though this has been made much more accessible with the emergence of open-source, extensible compiler frameworks such as LLVM. As a result, most innovation activity here happens within WG21, with some notable exceptions like Circle and Cpp2. Others have chosen to depart from the C++ language completely (Carbon, Hylo), so their potential impact on C++ standardization is remote at best.
• As for the standard library, the situation is more varied. These are some examples:
  
• Straight into the standard: <locale>.
  
• Straight into the standard, some prior art: IOStreams, STL, unordered associative containers.
  
• Straight into the standard, extensive prior art: std::string_view.
  
• Explicitly written for standardization, one reference implementation: mdspan.
• Explicitly written for standardization, various reference implementations: ranges, std::expected.
  
• Moderate to high level of prior field experience: Boost.Filesystem, Boost.Regex, Boost.SmartPtr, Boost.Thread, Boost.Tuple.
• Not initially intended for standardization, high level of prior field experience: {fmt}.

In general, the trend for the evolution of the standard library seems to be towards proposing new components straight into the standard with very little field experience.

Pros and cons of standardization

The history of C++ standardization has met with some resounding successes (STL, templates, concurrency, most vocabulary types) as well as failures (exported templates, GC support, exception specifications, std::auto_ptr)  and in-between scenarios (std::regex,  ranges).

Focusing on the standard library, we can identify benefits of standardization vs. having a separate, non-standard component:

• The level of exposure to C++ users increases dramatically. Some companies have bans on the usage of external libraries, and even if no bans are in place, consuming the standard library is much more convenient than having to manage external dependencies —though this is changing.
  
• Standardization ensures a high level of (system) portability, potentially beyond the reach of external library authors without access to exotic environments.
• For components with high interoperability potential (think vocabulary types), having them in the standard library guarantees that they become the tool of choice for API-level module integration.

But there are drawbacks as well that must be taken into consideration:

• The evolution of a library halts or reduces significantly once it is standardized. One major factor for this is WG21's self-imposed restriction to preserve backwards compatibility, and in particular ABI compatibility. For example:
  
• Defects on the API of std::function had to be fixed by adding a new std::copyable_function component.
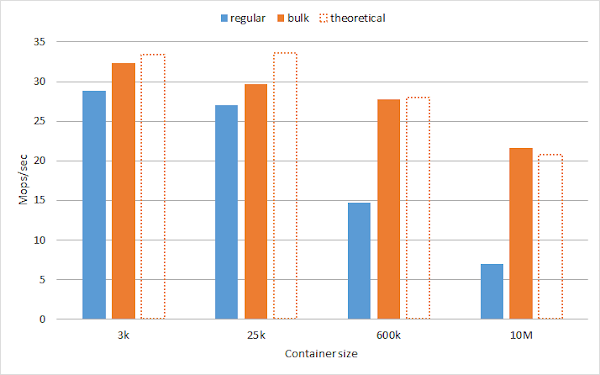
• Unordered associative containers were specified with the explicit assumption that they should be based on a technique known as separate chaining/closed addressing. The state of the art in this area has evolved spectacularly since 2003, and modern hash table implementations mostly use open addressing, which is de facto forbidden by the standard API, and outperform std::unordered_(map|set) by a large factor.
  

Another factor contributing to library freeze may be the lack of motivation from the authors once they succeed in getting their proposals accepted, as the process involved is very demanding and can last for years.

• Some libraries cover specialized domains that standard library implementors cannot be expected to master. Some cases in point:
• Current implementations of std::regex are notoriously slower than Boost.Regex, a situation aggravated by the need to keep ABI compatibility.
• Correct and efficient implementations of mathematical special functions require ample expertise in the area of numerical computation. As a result, Microsoft standard library implements these as mere wrappers over Boost.Math, and libc++ seems to be following suit. This is technically valid, but begs the question of what the standardization of these functions was useful for to begin with.
• Additions to the upcoming standard (as of this writing, C++26) don't benefit users immediately because the community typically lags behind by two or three revisions of the language.
  

So, standardizing a library component is not always the best course of action for the benefit of current and future users of that component. Back in 2001, Stroustrup remarked that "[p]eople sometime forget that a library doesn't have to be part of the standard to be useful", but, to this day, WG21 does not seem to have formal guidelines as to what constitutes a worthy addition to the standard, or how to engage with the community in a world of ever-expanding and more accessible external libraries. We would like to contribute some modest ideas in that direction.

An assessment model for library standardization

Going back to the basic principles of standards, the main benefits to be derived from standardizing a technology (in our case, a C++ library) are connected to higher compatibility and interoperability as a means to increase overall productivity (assumedly correlated to the level of usage of the library within the community). Leaving aside for the moment the size of the potential target audience, we identify two characteristics of a given library that make it suitable for standardization:

• Its portability requirements, defined as the level of coupling that an optimal implementation has with the underlying OS, CPU architecture, etc. The higher these requirements the more sense it makes to include the library as a mandatory part of the standard.
• Its interoperability potential, that is, how much the library is expected to be used as part of public APIs interconnecting different program modules vs. as a private implementation detail. A library with high interoperability potential is maximally useful when included in the common software "stack" shared by the community.

So, the baseline standardization value of a library, denoted V₀, can be modeled as:

V₀ = aP + bI,

where P denotes the library's portability requirements and I its interoperability potential. The figure shows the baseline standardization value of some library domains within the P-I plane. The color red indicates that this value is low, green that it is high.

A low baseline standardization value for a library does not mean that the library is not useful, but rather that there is little gain to be obtained from standardizing it as opposed to making it available externally. The locations of the exemplified domains in the P-I plane reflect the author's estimation and may differ from that of the reader.

Now, we have seen that the adoption of a library requires some prior field experience, defined as

E = T·U,

where T is the age of the library and U is average number of users.

• When E is very low, the library is not mature enough and standardizing it can result in a defective design that will be much harder to fix within the standard going forward; this effectively decreases the net value of standardization.
  
• On the contrary, if E is very high, which is correlated to the library having already reached its maximum target audience, the benefits of standardization are vanishingly small: most people are already using the library and including it into the official standard has little value added —the library has become a de facto standard.
  

So, we may expect to attain an optimum standardization opportunity S between the extremes E = 0 and E_max.

Finally, the net standardization value of a library is defined as

V = V₀·S·U_max,

where U_max is the library's maximum target audience. Being a conceptual model, the purpose of this framework is not so much to establish a precise evaluation formula as to help stakeholders raise the right questions when considering a library for standardization:

• How high are the library's portability requirements?
• How high its interoperability potential?
• Is it too immature yet? Does it have actual field experience?
  
• Or, on the contrary, has it already reached its maximum target audience?
• How big is this audience?
  

Boost, the standard and beyond

Boost was launched in 1998 upon the idea that "[a] world-wide web site containing a repository of free C++ class libraries would be of great benefit to the C++ community". Serving as a venue for future standardization was mentioned only as a secondary goal, yet very soon many saw the project as a launching pad towards the standard library, a perception that has changed since. We analyze the different stages of this 25+-year-old project in connection with its contributions to the standard and to the community.

Golden era: 1998-2011

In its first 14 years of existence, the project grew from 0 to 113 libraries, for a total uncompressed size of 324 MB. Out of these 113 libraries, 12 would later be included in C++11, typically with modifications (Array, Bind, Chrono, EnableIf, Function, Random, Ref, Regex, SmartPtr, Thread, Tuple, TypeTraits); it may be noted that, even at this initial stage, most Boost libraries were not standardized or meant for standardization. From the point of view of the C++ standard library, however, Boost was the first contributor by far. We may venture some reasons for this success:

• There was much low-hanging fruit in the form of small vocabulary types and obvious utilities.
  
• Maybe due to a combination of scarce competition and sheer luck, Boost positioned itself very quickly as the go-to place for contributing and consuming high-quality C++ libraries. This ensured a great deal of field experience with the project.
  
• Many of the authors of the most relevant libraries were also prominent figures within the C++ community and WG21.
  

Middle-age issues: 2012-2020

By 2020, Boost had reached 164 libraries totaling 717 MB in uncompressed size (so, the size of the average library, including source, tests and documentation, grew by 1.5 with respect to 2011). Five Boost libraries were standardized between C++14 and C++20 (Any, Filesystem, Math/Special Functions, Optional, Variant): all of these, however, were already in existence before 2012, so the rate of successful new contributions from Boost to the standard decreased effectively to zero in this period. There were some additional unsuccessful proposals (Mp11).

The transition of Boost from the initial ramp-up to a more mature stage met with several scale problems that impacted negatively the public perception of the project (and, to some extent that we haven't able to determine, its level of usage). Of particular interest is a public discussion that took place in 2022 on Reddit and touched on several issues more or less recognized within the community of Boost authors:

• The default/advertised way to consume Boost as a monolithic download introduces a bulky, hard to manage dependency on projects.
• B2, Boost's native build technology, is unfamiliar to users more accustomed to widespread tools such as CMake.
• Individual Boost libraries are perceived as bloated in terms of size, internal dependences and compile times. Alternative competing libraries are self-contained, easier to install and smaller as they rely on newer versions of the C++ standard.
• Many useful components are already provided by the standard library.
• There are great differences between libraries in terms of their quality; some libraries are all but abandoned.
• Documentation is not good enough, in particular if compared to cppreference.com, which is regarded as the golden standard in this area.
  

A deeper analysis reveals some root causes for this state of affairs:

• Overall, the Boost project is very conservative and strives not to break users' code on each version upgrade (even though, unlike the standard, backwards API/ABI compatibility is not guaranteed). In particular, many Boost authors are reluctant to increase the minimum C++ standard version required for their libraries. Also, there is no mechanism in place to retire libraries from the project.
• Supporting older versions of the C++ standard locks in some libraries with suboptimal internal dependencies, the most infamous being Boost.MPL, which many identify (with or without reason) as responsible for long compile times and cryptic error messages.
• Boost's distribution and build mechanisms were invented in an era where package managers and build systems were not prevalent. This works well for smaller footprints but presents scaling problems that were not foreseen at the beginning of the project.
• Ultimately, Boost is a federation of libraries with different authors and sensibilities. This fact accounts for the various levels of documentation quality, user support, maintenance, etc.
  

Some of these characteristics are not negative per se, and have in fact resulted in an extremely durable and available service to the C++ community that some may mistakenly take for granted. Supporting "legacy C++" users is, by definition, neglected by WG21, and maintaining libraries that were already standardized is of great value to those who don't live on the edge (and, in the case of the std::regex fiasco, those who do). Confronted with the choice of serving the community today vs. tomorrow (via standardization proposals), the Boost project took, perhaps unplannedly, the first option. This is not to say that all is good with the Boost project, as many of the problems found in 2012-2020 are strictly operational.

Evolution: 2021-2024 and the future

Boost 1.85 (April 2024) contains 176 libraries (7% increase with respect to 2020) and has a size of 731 MB (2% increase). Only one Boost component has partially contributed to the C++23 standard library (boost::container::flat_map), though there has been some unsuccessful proposals (the most notable being Boost.Asio).

In response to the operational problems we have described before, some authors have embarked on a number of improvement and modernization tasks:

• Beginning in Boost 1.82 (Apr 2023), some core libraries announced the upcoming abandonment of C++03 support as part of a plan to reduce code base sizes, maintenance costs, and internal dependencies on "polyfill" components. This initiative has a cascading effect on dependent libraries that is still ongoing.
  
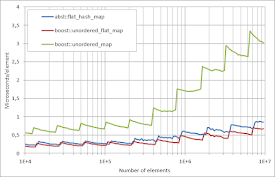
• Alongside C++03 support drop, many libraries have been updated to reduce the number of internal dependencies (that even were, in some cases, cyclic). The figure shows the cumulative histograms of the number of dependencies for Boost libraries in versions 1.66 (2017), 1.75 (2020) and 1.85 (2024):
  

• Official CMake support for the entire Boost project was announced in Oct 2023. This support also allows for downloading and building of individual libraries (and their dependencies).
  
• On the same front of modular consumption, there is work in progress to modularize B2-based library builds, which will enable package managers such as Conan to offer Boost libraries individually. vcpkg already offers this option.
• Starting in July 2023, boost.org includes a search widget indexing the documentation of all libraries. The ongoing MrDocs project seeks to provide a Doxygen-like tool for automatic C++ documentation generation that could eventually support Boost authors  —library docs are currently written more or less manually in a plethora of languages such as raw HTML, Quickbook, Asciidoc, etc. There is a new Boost website in the works scheduled for launch during mid-2024.
  

Where is Boost headed? It must be stressed again that the project is a federation of authors without a central governing authority in strategic matters, so the following should be taken as an interpretation of detected current trends:

• Most of the recently added libraries cover relatively specific application-level domains (networking/database protocols, parsing) or else provide utilities likely to be superseded by future C++ standards, as is the case with reflection (Describe, PFR). One library is a direct backport of a C++17 standard library component (Charconv). Boost.JSON provides yet another solution in an area already rich with alternatives external to the standard library. Boost.LEAF proposes an approach to error handling radically different to that of the latest standard (std::expected). Boost.Scope implements and augment a WG21 proposal currently on hold (<experimental/scope>).
  
• In some cases, standard compatibility has been abandoned to provide faster performance or richer functionality (Container, Unordered, Variant2).
  
• No new library supports C++03, which reduces drastically their number of internal dependencies (except in the case of networking libraries depending on Boost.Asio).
• On the other hand, most new libraries are still conservative in that they only require C++11/14, with some exceptions (Parser and Redis require C++17, Cobalt requires C++20).
• There are some experimental initiatives like the proposal to serve Boost libraries as C++ modules, which has been met with much interest and support from the Visual Studio team. An important appeal of this idea is that it will allow compiler vendors and the committee to obtain field experience from a large, non-trivial codebase.
  

The current focus of Boost seems then to have shifted from standards-bound innovation to higher-level and domain-specific libraries directly available to users of C++11/14 and later. More stress is increasingly being put on maintenance, reduced internal dependencies and modular availability, which further cements the thesis that Boost authors are more concerned about serving the C++ community from Boost itself than eventually migrating to the standard. There is still a flow of ideas from Boost to WG21, but they do not represent the bulk of the project activity.

Conclusions

Traditionally, the role of standardization has been to consolidate previous innovations that have reached maturity so as to maximize their potential for industry vendors and users. In the very specific case of programming languages, and WG21/LEWG in particular, the standards committee has taken on the role of innovator and is pushing the industry rather than adopting external advancements or coexisting with them. This presents some problems related to lack of field experience, limitations to internal evolution imposed by backwards compatibility and an associated workload that may exceed the capacity of the committee. Thanks to open developer platforms (GitHub, GitLab), widespread build systems (CMake) and package managers (Conan, vcpkg), the world of C++ libraries is richer and more available than ever. WG21 could reconsider its role as part of an ecosystem that thrives outside and alongside its own activity. We have proposed a conceptual evaluation model for standardization of C++ libraries that may help in the conversations around these issues. Boost has shifted its focus from being a primary venue for standardization to serving the C++ community (including users of previous versions of the language) through increasingly modular, high level and domain-specific libraries. Hopefully, the availability and reach of the Boost project will help gain much needed field experience that could eventually lead to further collaborations with and contributions to WG21 in a non-preordained way.

A case in API ergonomics for ordered containers

Suppose we have a std::set<int> and would like to retrieve the elements between values a and b, both inclusive. This task is served by operations std::set::lower_bound and std::set::upper_bound:

std::set<int> x=...;

// elements in [a,b]
auto first = x.lower_bound(a);
auto last  = x.upper_bound(b);
 
while(first != last) std::cout<< *first++ <<" ";

Why do we use lower_bound for the first iterator and upper_bound for the second? The well-known STL convention is that a range of elements is determined by two iterators first and last, where first points to the first element of the range and last points to the position right after the last element. This is done so that empty ranges can be handled without special provisions (first == last).

Now, with this convention in mind and considering that

• lower_bound(a) returns an iterator to the first element not less than a,
• upper_bound(b) returns an iterator to the first element greater than b,

we can convince ourselves that the code above is indeed correct. The situations where one or both of the interval endpoints are not inclusive can also be handled:

// elements in [a,b)
auto first = x.lower_bound(a);
auto last  = x.lower_bound(b);

// elements in (a,b]
auto first = x.upper_bound(a);
auto last  = x.upper_bound(b);

// elements in (a,b)
auto first = x.upper_bound(a);
auto last  = x.lower_bound(b);

but getting them right requires some thinking.

Boost.MultiIndex introduces the operation range to handle this type of queries:

template<typename LowerBounder,typename UpperBounder>
std::pair<iterator,iterator>
range(LowerBounder lower, UpperBounder upper);

lower and upper are user-provided predicates that determine whether an element is not to the left and not to the right of the considered interval, respectively. The formal specification of LowerBounder and UpperBounder is quite impenetrable, but using this facility, in particular in combination with Boost.Lambda2, is actually straightforward:

// equivalent to std::set<int>
boost::multi_index_container<int> x=...;

using namespace boost::lambda2;

// [a,b]
auto [first, last] = x.range(_1 >= a, _1 <= b);

// [a,b)
auto [first, last] = x.range(_1 >= a, _1 < b);

// (a,b]
auto [first, last] = x.range(_1 > a,  _1 <= b);

// (a,b)
auto [first, last] = x.range(_1 > a,  _1 < b);

The resulting code is much easier to read and to get right in the first place, and is also more efficient than two separate calls to [lower|upper]_bound   (because the two internal rb-tree top-to-bottom traversals can be partially joined in the implementation of range). Just as importantly, range handles situations such as this:

int a = 5;
int b = 2; // note a > b

// elements in [a,b]
auto first = x.lower_bound(a);
auto last  = x.upper_bound(b);
 
// undefined behavior
while(first != last) std::cout<< *first++ <<" ";

When a > b, first may be strictly to the right of last, and consequently the while loop will crash or never terminate. range, on the other hand, handles the situation gracefully and returns an empty range.

We have seen an example of how API design can help reduce programming errors and increase efficiency by providing higher-level facilities that model and encapsulate scenarios otherwise served by a combination of lower-level operations. It may be interesting to have range-like operations introduced for standard associative containers.

Bulk visitation in boost::concurrent_flat_map

• Introduction
• Prior art
• Bulk visitation design
• Performance analysis
• Conclusions and next steps

Introduction

boost::concurrent_flat_map and its boost::concurrent_flat_set counterpart are Boost.Unordered's associative containers for high-performance concurrent scenarios. These containers dispense with iterators in favor of a visitation-based interface:

boost::concurrent_flat_map<int, int> m;
...
// find the element with key k and increment its associated value
m.visit(k, [](auto& x) {
  ++x.second;
});

This design choice was made because visitation is not affected by some inherent problems afflicting iterators in multithreaded environments.

Starting in Boost 1.84, code like the following:

std::array<int, N> keys;
...
for(const auto& key: keys) {
  m.visit(key, [](auto& x) { ++x.second; });
}

can be written more succintly via the so-called bulk visitation API:

m.visit(keys.begin(), keys.end(), [](auto& x) { ++x.second; });

As it happens, bulk visitation is not provided merely for syntactic convenience: this operation is internally optimized so that it performs significantly faster than the original for-loop. We discuss here the key ideas behind bulk visitation internal design and analyze its performance.

Prior art

In their paper "DRAMHiT: A Hash Table Architected for the Speed of DRAM", Narayanan et al. explore some optimization techniques from the domain of distributed system as translated to concurrent hash tables running on modern multi-core architectures with hierarchical caches. In particular, they note that cache misses can be avoided by batching requests to the hash table, prefetching the memory positions required by those requests and then completing the operations asynchronously when enough time has passed for the data to be effectively retrieved. Our bulk visitation implementation draws inspiration from this technique, although in our case visitation is fully synchronous and in-order, and it is the responsibility of the user to batch keys before calling the bulk overload of boost::concurrent_flat_map::visit.

Bulk visitation design

As discussed in a previous article, boost::concurrent_flat_map uses an open-addressing data structure comprising:

• A bucket array split into 2ⁿ groups of N = 15 slots.
• A metadata array associating a 16-byte metadata word to each slot group, used for SIMD-based reduced-hash matching.
• An access array with a spinlock (and some additional information) for locked access to each group.

The happy path for successful visitation looks like this:

1. The hash value for the looked-up key and its mapped group position are calculated.
2. The metadata for the group is retrieved and matched against the hash value.
3. If the match is positive (which is the case for the happy path), the group is locked for access and the element indicated by the matching mask is retrieved and compared with the key. Again, in the happy path this comparison is positive (the element is found); in the unhappy path, more elements (within this group or beyond) need be checked.

(Note that happy unsuccessful visitation simply terminates at step 2, so we focus our analysis on successful visitation.) As the diagram shows, the CPU has to wait for memory retrieval between steps 1 and 2 and between steps 2 and 3 (in the latter case, retrievals of mutex and element are parallelized through manual prefetching). A key insight is that, under normal circumstances, these memory accesses will almost always be cache misses: successive visitation operations, unless for the very same key, won't have any cache locality. In bulk visitation, the stages of the algorithm are pipelined as follows (the diagram shows the case of three operations in the bulk batch):

The data required at step N+1 is prefetched at the end of step N. Now, if a sufficiently large number of operations are pipelined, we can effectively eliminate cache miss stalls: all memory addresses will be already cached by the time they are used.

The operation visit(first, last, f) internally splits [first, last) into chunks of bulk_visit_size elements that are then processed as described above. This chunk size has to be sufficiently large to give time for memory to be actually cached at the point of usage. On the upper side, the chunk size is limited by the number of outstanding memory requests that the CPU can handle at a time: in Intel architectures, this is limited by the size of the line fill buffer, typically 10-12. We have empirically confirmed that bulk visitation maxes at around bulk_visit_size = 16, and stabilizes beyond that.

Performance analysis

For our study of bulk visitation performance, we have used a computer with a Skylake-based Intel Core i5-8265U CPU:

	Size/core	Latency [ns]
L1 data cache	32 KB	3.13
L2 cache	256 KB	6.88
L3 cache	6 MB	25.00
DDR4 RAM		77.25

We measure the throughput in Mops/sec of single-threaded lookup (50/50 successful/unsuccessful) for both regular and bulk visitation on a boost::concurrent_flat_map<int, int> with sizes N = 3k, 25k, 600k, and 10M: for the three first values, the container fits entirely into L1, L2 and L3, respectively. The test program has been compiled with clang-cl for Visual Studio 2022 in release mode.

As expected, the relative performance of bulk vs. regular visitation grows as data is fetched from a slower cache (or RAM in the latter case). The theoretical throughput achievable by bulk visitation has been estimated from regular visitation by subtracting memory retrieval times as calculated with the following model:

• If the container fits in Ln (L4 = RAM), Ln−1 is entirely occupied by metadata and access objects (and some of this data spills over to Ln).
• Mutex and element retrieval times (which only apply to successful visitation) are dominated by the latter.

Actual and theoretical figures match quite well, which sugggests that the algorithmic overhead imposed by bulk visitation is negligible.

We have also run benchmarks under conditions more similar to real-life for boost::concurrent_flat_map, with and without bulk visitation, and other concurrent containers, using different compilers and architectures. As an example, these are the results for a workload of 50M insert/lookup mixed operations distributed across several concurrent threads for different data distributions with Clang 12 on an ARM64 computer:

5M updates, 45M lookups skew=0.01	5M updates, 45M lookups skew=0.5	5M updates, 45M lookups skew=0.99

Again, bulk visitation increases performance noticeably. Please refer to the benchmark site for further information and results.

Conclusions and next steps

Bulk visitation is an addition to the interface of boost::concurrent_flat_map and boost::concurrent_flat_set that improves lookup performance by pipelining the internal visitation operations for chunked groups of keys. The tradeoff for this increased throughput is higher latency, as keys need to be batched by the user code before issuing the visit operation.

The insights we have gained with bulk visitation for concurrent containers can be leveraged for future Boost.Unordered features:

• In principle, insertion can also be made to operate in bulk mode, although the resulting pipelined algorithm is likely more complex than in the visitation case, and thus performance increases are expected to be lower.
• Bulk visitation (and insertion) is directly applicable to non-concurrent containers such as boost::unordered_flat_map: the main problem for this is one of interface design because we are not using visitation here as the default lookup API (classical iterator-based lookup is provided instead). Some possible options are:
  1. Use visitation as in the concurrent case.
  2. Use an iterator-based lookup API that outputs the resulting iterators to some user-provided buffer (probably modelled as an output "meta" iterator taking container iterators).

Bulk visitation will be officially shipping in Boost 1.84 (December 2023) but is already available by checking out the Boost.Unordered repo. If you are interested in this feature, please try it and report your local results and suggestions for improvement. Your feedback on our current and future work is much welcome.