Measuring lookup times for C++ unordered associative containers

This is the final installment of our series of entries on the performance of C++ unordered associative containers as implemented by Dinkumware, Boost.Unordered and Boost.MultiIndex. We now analyze lookup according to the following two scenarios:

void successful_lookup(const container& c,unsigned int n)
{
  while(n--)s.find(rnd());
}

void unsuccessful_lookup(const container& c,unsigned int n)
{
  while(n--)s.find(rnd2());
}

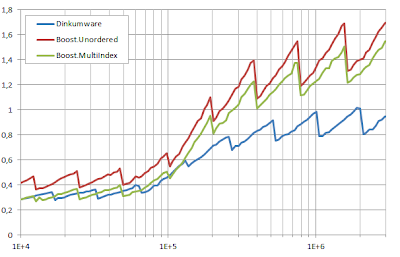
where rnd generates the same random sequence of values used to populate c with n elements and rnd2 is a different, statistically independent sequence: so, lookups in the fist scenario always succeed, while those in the second one are very likely to fail. As usual we provide profiling programs for the non-duplicate and duplicate versions of the containers, the build and test environment stays the same as before (Microsoft Visual Studio 2012, default release mode settings, Windows box with an Intel Core i5-2520M CPU @2.50GHz), times are in microseconds/element, n runs from 10,000 to 3 million. The results for the non-duplicate case are depicted in the figure (first successful lookup, then unsuccessful):

The algorithms implemented by the three libraries are entirely similar (invoke hash function, map to bucket, traverse till either a matching element or the end of the bucket is met); the differences we see in performance are explained by these two factors:

• Dinkumware, as we have discussed in a previous entry, has the fastest hash→bucket mapping.
• Boost.Unordered and Boost.MultiIndex use the same approach to locate the bucket to search through, namely mapping hash values to bucket entries with an expensive modulo calculation and getting to the bucket via the preceding element (thus worsening locality with respect to Dinkumware's procedure): Boost.Unordered calculates this modulo slightly less inefficiently and, in unsuccessful lookups, often has to do the calculation twice, the first time to locate the bucket, and the second one to determine when that bucket ends (if it is not empty).  

The duplicate case with average group size G = 5 and maximum load factor F_max = 1 looks like this (first successful lookup, then unsuccessful):

For both scenarios, Dinkumware's performance degrades more than the other two libs with respect to the non-duplicate case: when a collision happens, i.e. if a different group than searched for is found in the bucket, Dinkumware has to check every element of the group, whereas Boost.Unordered and Boost.MultiIndex take advantage of their group-skipping capabilities. Boost.MultiIndex has a poorer group-skipping mechanism as it only applies to groups with size > 2, which is more apparent on unsuccessful lookups (for successful lookups the probability that two groups end up in the same bucket is very small.)

Lastly, this is the situation when we set F_max = 5 (first successful lookup, then unsuccessful):

Now the disadvantage of Dinkumware is much more clear: with a typical load F = 0.75·F_max =3.75, the average number of elements checked is 1+ F/2 =  2.875 for successful lookups and F = 3.75 for unsuccessful ones, while for Boost.Unordered the corresponding numbers are 1+ F/2G = 1.375 and F/G = 0.75, respectively, and slightly worse than these for Boost.MultiIndex as this library does not perform group skipping for group sizes ≤ 2.