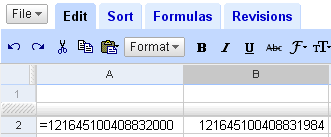
Of course 19! is not 121645100408831984, but 121645100408832000, off by 16. The puzzlement continued when I wrote:
Though the values at B2 and B3 are displayed differently, they compare the same. What's going on here? Actually, B3 is not holding a number but the string "121645100408832000", hence its left alignment --numbers are displayed right-aligned by default. Once we force "121645100408832000" to be internally translated to a number the glitch reappears; it suffices to enter the value as "=121645100408832000":
After thinking a bit about it I realized the value 19! has 57 binary digits, and this rang a bell: if values were stored in double precision IEEE 754 format, with fraction width of 52 bits, not all integers greater than 253 would have exact representation, and in fact 253 + 1 would be the first non-representable integer:
The figure above seems to confirm the hypothesis. For 224 +1 the representation is exact, which seems to rule out single precision IEEE 754 with its 23 bit fraction. In fact, I tested all the values 2n + 1 for n = 1,...,54, and the representation is exact except for n = 54. Further confirmation of the double precision IEEE 754 hypothesis comes from the following:
Does this explain it all? Well, not entirely. The binary representation of 19! is
110110000001010111001001100000110100010010000000000000000.
Thanks to the 16 trailing zeros, this is exactly representable in double precision IEEE 754 as:
19! = s·2e − 1023·1.f,
s = 0,
e = 100001101112 = 1079 = 56 + 1023,
f = 10110000001010111001001100000110100010010000000000002.
So there must be additional problems apart from the loss of precision due to the use of floating point. We will investigate the issue further in a later entry.




No comments :
Post a Comment