- Introduction
- The case for open addressing
boost::unordered_flat_mapdata structure- Rehashing
- Hash post-mixing
- Statistical properties of
boost::unordered_flat_map - Benchmarks
- Deviations from the standard
- Conclusions and next steps
Starting in Boost 1.81 (December 2022), Boost.Unordered
provides, in addition to its previous implementations of C++ unordered associative containers,
the new containers boost::unordered_flat_map and boost::unordered_flat_set (for the sake
of brevity, we will only refer to the former in the remaining of this article).
If boost::unordered_map strictly adheres to the C++ specification for std::unordered_map,
boost::unordered_flat_map deviates in a number of ways from the standard
to offer dramatic performance improvements in exchange; in fact, boost::unordered_flat_map
ranks amongst the fastest hash containers currently available to C++ users.
We describe the internal structure of boost::unordered_flat_map and provide
theoretical analyses and benchmarking data to help readers gain insights into
the key design elements behind this container's excellent performance.
Interface and behavioral differences with the standard are also discussed.
We have previously discussed why
closed addressing was chosen back in 2003 as the implicit layout for std::unordered_map.
20 years after, open addressing
techniques have taken the lead in terms of performance, and the fastest hash containers in the market
all rely on some variation of open addressing, even if that means that some deviations have to be introduced
from the baseline interface of std::unordered_map.
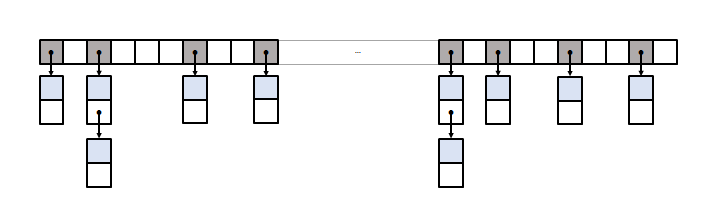
The defining aspect of open addressing is that elements are stored directly within the bucket array (as opposed to closed addressing, where multiple elements can be held into the same bucket, usually by means of a linked list of nodes). In modern CPU architectures, this layout is extremely cache friendly:
- There's no indirection needed to go from the bucket position to the element contained.
- Buckets are stored contiguously in memory, which improves cache locality.
The main technical challenge introduced by open addressing is what to do when elements are mapped into the same bucket, i.e. when a collision happens: in fact, all open-addressing variations are basically characterized by their collision management techniques. We can divide these techniques into two broad classes:
- Non-relocating: if an element is mapped to an occupied bucket, a probing sequence is started from that position until a vacant bucket is located, and the element is inserted there permanently (except, of course, if the element is deleted or if the bucket array is grown and elements rehashed). Popular probing mechanisms are linear probing (buckets inspected at regular intervals), quadratic probing and double hashing. There is a tradeoff between cache locality, which is better when the buckets probed are close to each other, and average probe length (the expected number of buckets probed until a vacant one is located), which grows larger (worse) precisely when probed buckets are close —elements tend to form clusters instead of spreading uniformly throughout the bucket array.
- Relocating: as part of the search process for a vacant bucket, elements can be moved from their position to make room for the new element. This is done in order to improve cache locality by keeping elements close to their "natural" location (that indicated by the hash → bucket mapping). Well known relocating algorithms are cuckoo hashing, hopscotch hashing and Robin Hood hashing.
If we take it as an important consideration to stay reasonably close to the original behavior
of std::unordered_map, relocating techniques pose the problem that insert may invalidate
iterators to other elements (so, they work more like std::vector::insert).
On the other hand, non-relocating open addressing faces issues on deletion: lookup starts at the original hash → bucket position and then keeps probing till the element is found or probing terminates, which is signalled by the presence of a vacant bucket:
So, erasing an element can't just restore its holding bucket as vacant, since that would preclude lookup from reaching elements further down the probe sequence:
A common techique to deal with this problem is to label buckets previously containing an element with a tombstone marker: tombstones are good for inserting new elements but do not stop probing on lookup:
Note that the introduction of tombstones implies that the average lookup probe length of the container won't decrease on deletion —again, special measures can be taken to counter this.
SIMD technologies, such as SSE2 and
Neon,
provide advanced CPU instructions for parallel arithmetic and logical operations
on groups of contiguous data values: for instance, SSE2 _mm_cmpeq_epi8 takes two packs of 16 bytes and compares
them for equality pointwise, returning the result as another pack of bytes. Although
SIMD was originally meant for acceleration of multimedia processing applications,
the implementors of some unordered containers, notably Google's
Abseil's Swiss tables and
Meta's F14, realized
they could leverage this technology to improve lookup times in hash tables.
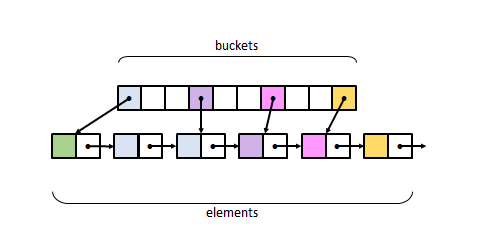
The key idea is to maintain, in addition to the bucket array itself, a separate metadata array holding reduced hash values (usually one byte in size) obtained from the hash values of the elements stored in the corresponding buckets. When looking up for an element, SIMD can be used on a pack of contiguous reduced hash values to quickly discard non-matching buckets and move on to full comparison for matching positions. This technique effectively checks a moderate number of buckets (16 for Abseil, 14 for F14) in constant time. Another beneficial effect of this approach is that special bucket markers (vacant, tombstone, etc.) can be moved to the metadata array —otherwise, these markers would take up extra space in the bucket itself, or else some representation values of the elements would have to be restricted from user code and reserved for marking purposes.
boost::unordered_flat_map data structure |
boost::unordered_flat_map's bucket array is logically split into 2n
groups of N = 15 buckets, and has a companion metadata array consisting of
2n 16-byte words. Hash mapping is done at the group level rather than
on individual buckets: so, to insert an element with hash value h, the group
at position h / 2W − n is selected and its first available bucket
used (W is 64 or 32 depending on whether the CPU architecture is 64- or 32-bit,
respectively); if the group is full, further groups are checked using a quadratic
probing sequence.
The associated metadata is organized as follows (least significant byte depicted rightmost):
hi holds information about the i-th bucket of the group:
- 0 if the bucket is empty,
- 1 to signal a sentinel (a special value at the end of the bucket array used to finish container iteration).
- otherwise, a reduced hash value in the range [2, 255] obtained from the least significant byte of the element's hash value.
When looking up within a group for an element with hash value h, SIMD operations, if available, are used to match the reduced value of h against the pack of values {h0, h1, ... , h14}. Locating an empty bucket for insertion is equivalent to matching for 0.
ofw is the so-called overflow byte: when inserting an element with hash value h, if the group is full then the (h mod 8)-th bit of ofw is set to 1 before moving to the next group in the probing sequence. Lookup probing can then terminate when the corresponding overflow bit is 0. Note that this procedure removes the need to use tombstones.
If neither SSE2 nor Neon is available on the target architecture, the logical organization of metadata stays the same, but information is mapped to two physical 64-bit words using bit interleaving as shown in the figure:
Bit interleaving allows for a reasonably fast implementation of matching operations in the absence of SIMD.
The maximum load factor of boost::unordered_flat_map is 0.875 and can't be changed
by the user. As discussed previously, non-relocating open addressing has the problem
that average probe length doesn't decrease on deletion when the erased elements
are in mid-sequence: so, continously inserting and erasing elements without triggering
a rehash will slowly degrade the container's performance; we call this phenomenon
drifting. boost::unordered_flat_map introduces the following anti-drift mechanism:
rehashing is controled by the container's maximum load, initially 0.875 times the
size of the bucket array; when erasing an element whose associated overflow bit is not
zero, the maximum load is decreased by one. Anti-drift guarantees that rehashing
will be eventually triggered in a scenario of repeated insertions and deletions.
It is well known that open-addressing containers require that the hash function be of good quality, in the sense that close input values (for some natural notion of closeness) are mapped to distant hash values. In particular, a hash function is said to have the avalanching property if flipping a bit in the physical representation of the input changes all bits of the output value with probability 50%. Note that avalanching hash functions are extremely well behaved, and less stringent behaviors are generally good enough in most open-addressing scenarios.
Being a general-purpose container, boost::unordered_flat_map does not impose any
condition on the user-provided hash function beyond what is required by the C++
standard for unordered associative containers. In order to cope with poor-quality
hash functions (such as the identity for integral types), an automatic bit-mixing stage
is added to hash values:
- 64-bit architectures: we use the
xmxfunction defined in Jon Maiga's "The construct of a bit mixer". - 32-bit architectures: the chosen mixer has been automatically generated by Hash Function Prospector and selected as the best overall performer in internal benchmarks. Score assigned by Hash Prospector: 333.7934929677524.
There's an opt-out mechanism available to end users so that avalanching hash functions
can be marked as such and thus be used without post-mixing. In particular,
the specializations of boost::hash
for string types are marked as avalanching.
boost::unordered_flat_mapWe have written a simulation program
to calculate some statistical properties
of boost::unordered_flat_map as compared with Abseil's absl::flat_hash_map,
which is generally regarded as one of the fastest hash containers available.
For the purposes of this analysis, the main design characteristics of
absl::flat_hash_map are:
- Bucket array sizes are of the form 2n, n ≥ 4.
- Hash mapping is done at the bucket level (rather than at the group
level as in
boost::unordered_flat_map). - Metadata consists of one byte per bucket, where the most significant bit is set to 1 if the bucket is empty, deleted (tombstone) or a sentinel. The remaining 7 bits hold the reduced hash value for occupied buckets.
- Lookup/insertion uses SIMD to inspect the 16 contiguous buckets beginning at the hash-mapped position, and then continues with further 16-bucket groups using quadratic probing. Probing ends when a non-full group is found. Note that the start positions of these groups are not aligned modulo 16.
The figure shows:
- the probability that a randomly selected group is full,
- the average number of hops (i.e. the average probe length minus one) for successful and unsuccessful lookup
as functions of the load factor, with perfectly random input and without intervening
deletions. Solid line is boost::unordered_flat_map, dashed line is
absl::flat_hash_map.
Some observations:
- Pr(group is full) is higher for
boost::unordered_flat_map. This follows from the fact that free buckets cluster at the end of 15-aligned groups, whereas forabsl::flat_hash_mapfree buckets are uniformly distributed across the array, which increases the probability that a contiguous 16-bucket chunk contains at least one free position. Consequently, E(num hops) for successful lookup is also higher inboost::unordered_flat_map. - By contrast, E(num hops) for unsuccessful lookup is considerably lower
in
boost::unordered_flat_map:absl::flat_hash_mapuses an all-or-nothing condition for probe termination (group is non-full/full), whereasboost::unordered_flat_mapuses the 8 bits of information in the overflow byte to allow for more finely-grained termination —effectively, making probe termination ~1.75 times more likely. The overflow byte acts as a sort of Bloom filter to check for probe termination based on reduced hash value.
The next figure shows the average number of actual comparisons (i.e. when
the reduced hash value matched) for successful and unsuccessful lookup.
Again, solid line is boost::unordered_flat_map and
dashed line is absl::flat_hash_map.
E(num cmps) is a function of:
- E(num hops) (lower better),
- the size of the group (lower better),
- the number of bits of the reduced hash value (higher better).
We see then that boost::unordered_flat_map approaches absl::flat_hash_map on
E(num cmps) for successful lookup (1% higher or less), despite its poorer
E(num hops) figures: this is so because boost::unordered_flat_map
uses smaller groups (15 vs. 16) and, most importantly, because its reduced
hash values contain log2(254) = 7.99 bits vs. 7 bits in absl::flat_hash_map,
and each additional bit in the hash reduced value decreases the number of negative
comparisons roughly by half. In the case of E(num cmps) for unsuccessful lookup,
boost::unordered_flat_map figures are up to 3.2 times lower under
high-load conditions.
We have measured the execution times of boost::unordered_flat_map against
absl::flat_hash_map and boost::unordered_map for basic operations
(insertion, erasure during iteration, successful lookup, unsuccessful lookup) with
container size n ranging from 10,000 to 10M. We provide the full benchmark code and
results for different 64- and 32-bit architectures in a
dedicated repository;
here, we just show the plots for GCC 11 in x64 mode on an
AMD EPYC Rome 7302P @ 3.0GHz.
Please note that each container uses its own default hash function, so a direct
comparison of execution times may be slightly biased.
|

|
|---|---|
| Running insertion | Running erasure |

|
 |
|---|---|
| Successful lookup | Unsuccessful lookup |
As predicted by our statistical analysis, boost::unordered_flat_map is
considerably faster than absl::flat_hash_map for unsuccessful lookup
because the average probe length and number of (negative) comparisons are
much lower; this effect translates also to insertion, since insert needs
to first check that the element is not present, so it internally performs an
unsuccessful lookup. Note how performance is less impacted (stays flatter)
when the load factor increases.
As for successful lookup, boost::unordered_flat_map is still faster, which may be
due to its better cache locality, particularly for low load factors: in this
situation, elements are clustered at the beginning portion of each group, while for
absl::flat_hash_map they are uniformly distributed with more empty space
in between.
boost::unordered_flat_map is slower than absl::flat_hash_map for runnning
erasure (erasure of some elements during container traversal). The actual culprit
here is iteration, which is particularly slow; this is a collateral effect
of having SIMD operations work only on 16-aligned metadata words, while
absl::flat_hash_map iteration looks ahead 16 metadata bytes beyond the current
iterator position.
Boost.Unordered provides a series of benchmarks
emulating real-life scenarios combining several operations for a number of
hash containers and key types (std::string, std::string_view, std::uint32_t,
std::uint64_t and a UUID class of size 16). The interested reader can
build and run the benchmarks on her environment of choice; as an example, these are
the results for GCC 11 in x64 mode on an Intel Xeon E5-2683 @ 2.10GHz:
std::string std::unordered_map: 38021 ms, 175723032 bytes in 3999509 allocations boost::unordered_map: 30785 ms, 149465712 bytes in 3999510 allocations boost::unordered_flat_map: 14486 ms, 134217728 bytes in 1 allocations multi_index_map: 30162 ms, 178316048 bytes in 3999510 allocations absl::node_hash_map: 15403 ms, 139489608 bytes in 3999509 allocations absl::flat_hash_map: 13018 ms, 142606336 bytes in 1 allocations std::unordered_map, FNV-1a: 43893 ms, 175723032 bytes in 3999509 allocations boost::unordered_map, FNV-1a: 33730 ms, 149465712 bytes in 3999510 allocations boost::unordered_flat_map, FNV-1a: 15541 ms, 134217728 bytes in 1 allocations multi_index_map, FNV-1a: 33915 ms, 178316048 bytes in 3999510 allocations absl::node_hash_map, FNV-1a: 20701 ms, 139489608 bytes in 3999509 allocations absl::flat_hash_map, FNV-1a: 18234 ms, 142606336 bytes in 1 allocations
std::string_view std::unordered_map: 38481 ms, 207719096 bytes in 3999509 allocations boost::unordered_map: 26066 ms, 181461776 bytes in 3999510 allocations boost::unordered_flat_map: 14923 ms, 197132280 bytes in 1 allocations multi_index_map: 27582 ms, 210312120 bytes in 3999510 allocations absl::node_hash_map: 14670 ms, 171485672 bytes in 3999509 allocations absl::flat_hash_map: 12966 ms, 209715192 bytes in 1 allocations std::unordered_map, FNV-1a: 45070 ms, 207719096 bytes in 3999509 allocations boost::unordered_map, FNV-1a: 29148 ms, 181461776 bytes in 3999510 allocations boost::unordered_flat_map, FNV-1a: 15397 ms, 197132280 bytes in 1 allocations multi_index_map, FNV-1a: 30371 ms, 210312120 bytes in 3999510 allocations absl::node_hash_map, FNV-1a: 19251 ms, 171485672 bytes in 3999509 allocations absl::flat_hash_map, FNV-1a: 17622 ms, 209715192 bytes in 1 allocations
std::uint32_t std::unordered_map: 21297 ms, 192888392 bytes in 5996681 allocations boost::unordered_map: 9423 ms, 149424400 bytes in 5996682 allocations boost::unordered_flat_map: 4974 ms, 71303176 bytes in 1 allocations multi_index_map: 10543 ms, 194252104 bytes in 5996682 allocations absl::node_hash_map: 10653 ms, 123470920 bytes in 5996681 allocations absl::flat_hash_map: 6400 ms, 75497480 bytes in 1 allocations
std::uint64_t std::unordered_map: 21463 ms, 240941512 bytes in 6000001 allocations boost::unordered_map: 10320 ms, 197477520 bytes in 6000002 allocations boost::unordered_flat_map: 5447 ms, 134217728 bytes in 1 allocations multi_index_map: 13267 ms, 242331792 bytes in 6000002 allocations absl::node_hash_map: 10260 ms, 171497480 bytes in 6000001 allocations absl::flat_hash_map: 6530 ms, 142606336 bytes in 1 allocations
uuid std::unordered_map: 37338 ms, 288941512 bytes in 6000001 allocations boost::unordered_map: 24638 ms, 245477520 bytes in 6000002 allocations boost::unordered_flat_map: 9223 ms, 197132280 bytes in 1 allocations multi_index_map: 25062 ms, 290331800 bytes in 6000002 allocations absl::node_hash_map: 14005 ms, 219497480 bytes in 6000001 allocations absl::flat_hash_map: 10559 ms, 209715192 bytes in 1 allocations
Each container uses its own default hash function, except the entries labeled
FNV-1a in std::string and std::string_view, which use the same
implementation of
Fowler–Noll–Vo hash, version 1a,
and uuid, where all containers use the same user-provided function based on
boost::hash_combine.
The adoption of open addressing imposes a number of deviations from the C++
standard for unordered associative containers. Users should keep them in mind
when migrating to boost::unordered_flat_map from boost::unordered_map (or
from any other implementation of std::unordered_map):
- Both
KeyandTinboost::unordered_flat_map<Key,T>must be MoveConstructible. This is due to the fact that elements are stored directly into the bucket array and have to be transferred to a new block of memory on rehashing; by contrast,boost::unordered_mapis a node-based container and elements are never moved once constructed. - For the same reason, pointers and references to elements become invalid after
rehashing (
boost::unordered_maponly invalidates iterators). begin()is not constant-time (the bucket array is traversed till the first non-empty bucket is found).erase(iterator)returnsvoidrather than an iterator to the element after the erased one. This is done to maximize performance, as locating the next element requires traversing the bucket array; if that element is absolutely required, theerase(iterator++)idiom can be used. This performance issue is not exclusive to open addressing, and has been discussed in the context of the C++ standard too.- The maximum load factor can't be changed by the user (
max_load_factor(z)is provided for backwards compatibility reasons, but does nothing). Rehashing can occur before the load reachesmax_load_factor() * bucket_count()due to the anti-drift mechanism described previously. - There is no bucket API (
bucket_size,begin(n), etc.) savebucket_count. - There are no node handling facilities (
extract, etc.) Such functionality makes no sense here as open-addressing containers are precisely not node-based.mergeis provided, but the implementation relies on element movement rather than node transferring.
boost::unordered_flat_map and boost::unordered_flat_set are the new
open-addressing containers in Boost.Unordered providing top speed
in exchange for some interface and behavioral deviations from the standards-compliant
boost::unordered_map and boost::unordered_set. We have analyzed their
internal data structure and provided some theoretical and practical evidence
for their excellent performance. As of this writing, we claim
boost::unordered_flat_map/boost::unordered_flat_set
to rank among the fastest hash containers available to C++ programmers.
With this work, we have reached an important milestone in the ongoing Development Plan for Boost.Unordered. After Boost 1.81, we will continue improving the functionality and performance of existing containers and will possibly augment the available container catalog to offer greater freedom of choice to Boost users. Your feedback on our current and future work is much welcome.