Suppose a company's HR department wishes to establish a statistical model for their personnel performance in order to set up outcome predictions for the company's bonus system. It is all too easy to assume that performance will follow a normal distribution such as this:
 Fig. 1: Performance distribution under the Bell Curve assumption.
Fig. 1: Performance distribution under the Bell Curve assumption.
The assumption stems from the deeply held custom in Psychology and Sociology of using the Bell Curve to model any a priori unknown human trait. Actually, if the company's hiring process is indeed efficient in selecting better than average people, this assumption is a complete contradiction.
Consider a simplistic hiring process in which performance is assesed by means of a test, so that applicants scoring some fixed minimum at the test are hired, and let us concede for the sake of the argument that the test is a perfect predictor of performance. The resulting performance distribution is depicted at the figure.
 Fig. 2: Performance distribution with a test-based selection process.
Fig. 2: Performance distribution with a test-based selection process.
The distribution has positive skewness, i.e. its right tail is longer than the left tail. So, the normal approximation with the same mean and variance (shown in dotted line) both overestimates low performers and underestimates high performers. It also underestimates low-to-normal performers and overestimates normal-to-high performers.
In other hiring process scenario, the best among N candidates is selected. The resulting distribution is depicted at the following figure for N = 10.
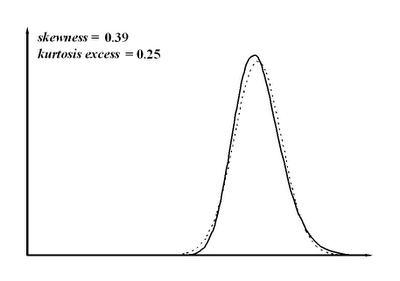 Fig. 3: Performance distribution with best-of-10 selection process.
Fig. 3: Performance distribution with best-of-10 selection process.
We have positive skewness again, though not as marked as in the prvious case. Skewness grows as N does. Again, the normal approximation results in overestimation of low performers and underestimation of high performers.
Finally, we consider a two-stage hiring process where applicants are first filtered by a test and then the best candidate out of N is selected.
 Fig. 4: Performance distribution with test prefiltering and best-of-10 selection process.
Fig. 4: Performance distribution with test prefiltering and best-of-10 selection process.
The test filter results in a slightly larger positive skewness. As in previous cases, normal approximation predicts more low performers and less high performers than the real case.
To summarize: hiring process not only results in a personnel performance distribution with a higher than average mean (which is the primary purpose of any hiring process); the distribution will also have positive skewness, with more excellent and less deficient people than predicted by the Bell Curve.



