This summer in Spain has been so particularly hot that people came up with graphical jokes like this:
(Cáceres is my hometown; versions of this picture for many other Spanish populations swarm the net.) Pursuing this idea half-seriously, one can reason that an increase in global temperatures due to climate change might be journalistically equated with the Earth getting closer to the Sun and thus receiving more radiation, which analogy conjures up doomy visions of our planet falling into the blazing hell of the star: let us do the calculations.
Climate sensitivity, usually denoted by λ, links changes in global surface temperature with variations of received radiative power
ΔT = λ ΔW.
The mechanism by which radiative power changes (increased albedo, greenhouse effect) results in a different associated λ parameter. For the case of power variations due to changes in solar activity, Tung et. al have calculated λs to be in the range of 0.69 to 0.97 K/(W/m2) using data from observations of 11-year solar cycles, and estimate that the stationary sensitivity (i.e. if the change in power was permanent) would be 1.5 times higher, thus in the range of 1.03 to 1.45 K/(W/m2).
Now, the Earth is D0 = 1.496 × 108 km away from the Sun, and receives an average radiation of W0 = 1366 W/m2. Assuming far-field conditions, the radiative power received at the Earth as a function of the distance D to the Sun is then
W = w / D2,
w = 3.057 × 1025 W/sr,
w = 3.057 × 1025 W/sr,
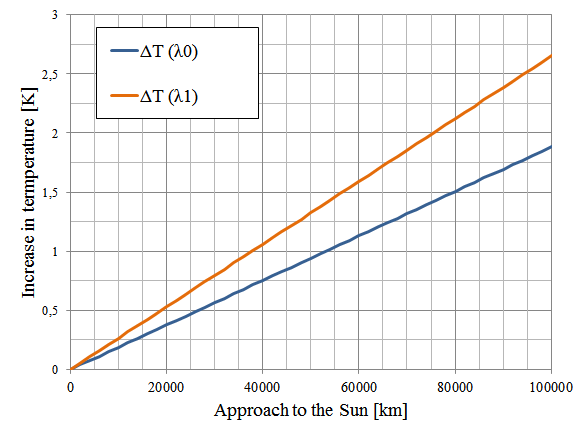
which allows us to calculate ΔT = λs ΔW from ΔD = D0 − D, as shown in the graph for the minimum and maximum estimated values of λs. Although this cannot be checked visually, the lines are not straight but include a negligible (in these distance ranges) quadratic component.
So, the estimated increase of 0.75 °C in global temperature during the 20th century is equivalent to pushing the Earth between 30 and 40 thousand kilometers towards the Sun. Each extra °C brings us 38,000-54,000 km closer to the star. For those stuck with USCS, each °F is equivalent to 13,000-18,000 miles.
As an alarmist meme, the figure works poorly since no amount of global warming will translate to anything resembling "falling into the Sun": relative changes in distance measure in the permyriads. And, yes, the joke at the beginning of this article is definitely a gross exaggeration.